How To Find The Perimeter/Circumference, Surface Area, And Water Volume Of A Swimming Pool

Understanding the various dimensions of your swimming pool is important when you are purchasing covers and other accessories. You also need to know the volume to properly treat the pool with chemicals. Some common measurements you may want to know:

• Circumference or perimeter of the pool
• Surface area of the water
• Water volume contained by the pool.

The specific formulas used to derive these measurements will vary, depending on the shape of the pool, and calculations can be easy or difficult, depending on that shape. A rectangular pool that is consistent in depth in all areas, for example, is pretty easy to measure, while an irregular curved shape may be considerably more difficult.

In some cases, measurements of water volume may be a careful estimate rather than a precise measurement or calculation. But there are a number of basic mathematical formulas that will give you fairly accurate determinations of the important measurements.

Some measurements require just a tape measure, while others are calculations based on those measurements. It is best to make your measurements in feet and fractions of feet. Rather than measuring the length of a pool as 30 feet 3 inches, for example, measure it as 30.25 feet.

The perimeter of your pool (or the circumference, if your pool is perfectly round) is a measurement that does not have many uses all by itself, but it may be helpful when you're making other calculations. The perimeter is easy to measure with an ordinary tape measure.

Rectangular or Square Pool

With a square or rectangular pool, you can, of course, measure each of the four sides and add the measurements together to determine the complete perimeter, though what is really necessary is to measure only one side of square pool, then multiply by 4.

With a rectangular pool, you can measure one short side, then multiply times 2; then measure the long side and multiply times 2 — and then add these measurements together to determine the complete perimeter.

For example, a rectangular pool that is 20 feet on one side and 40 feet on the other side could have its perimeter calculated like as: (20 x 2) + (40 x 2) = 120 feet.

Round Pool

A round swimming pool can also be measured by laying a tape measure around the outside edge of the pool. However, if you already know the diameter of the pool — which is the way many above-ground swimming pools are sold — you can determine the circumference with the formula: "Circumference = pi x diameter." For the sake of this calculation, you can use 3.14 as the value for pi. So, a round pool with a 20-foot diameter has a circumference of 3.14 x 20, or 62.8 feet.

Irregular Curved Pool

Here, too, the best method (really the only practical method) is to lay out a tape measure along the edge of the pool, as close to the water as you can. Other means of calculating the perimeter of an irregular pool are complicated.

Surface area is an important measurement that comes into play when you want to calculate water volume, or when buying a swimming pool cover. It is easy enough to calculate the surface area of a round, square or rectangular pool, but a little tricky with an irregular, curved pool.

Rectangular or Square Pool

With a square or rectangular shape, the formula for calculating area is simply to multiply length times width. So a pool that is 40 feet long and 30 feet wide will have a surface area of 1,200 square feet (40 x 30).

Round Pool

The formula for the area of a circle is "pi x r² " where "r" is the radius of the circle. So if you have a pool with a diameter of 20 feet, the radius is 10 feet, and the formula would be calculated in this way: 3.14 x 10² = 314 square feet.

Irregular Curved Pool

Bryan Trandem

Things get a little complicated when you are trying to calculate the surface area of a pool with a kidney shape or another irregular curved shape. The easiest way to approximate the surface area is by sketching the pool shape on graph paper, using a scale in which a 1/4-inch square represents 1 foot. By simply counting the number of squares occupied by the kidney shape, you can closely estimate the surface area of your pool.

The essence of calculating water volume is to take the surface area and multiply it by the depth of the pool. This calculation will give you the volume of a pool in cubic feet. But a pool volume is usually measured in gallons, so to convert the cubic footage to gallons, simply multiply the cubic footage measurement by 7.48. (A single cubic foot of water contains 7.48 gallons.)

Rectangular or Square Pool

With a perfectly square or rectangular pool that is a consistent depth at every point, the calculation can be formulated as "S x D = V," where S represents the surface area and D represent depth. So a pool that has a surface area of 1,200 square feet and is 6 feet deep holds 7,200 cubic feet of water.

To convert to gallons, multiply this number by 7.48. In this example, a pool with 7,200 cubic feet of water holds 53,856 gallons.

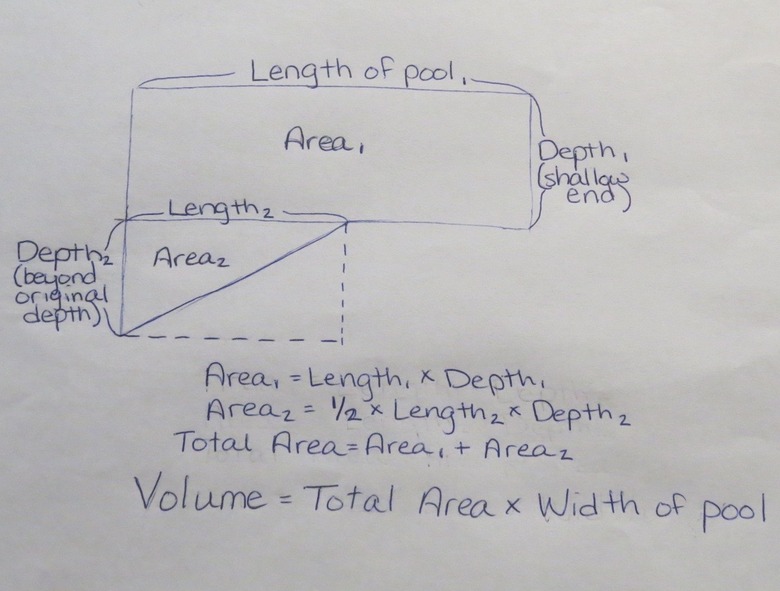
What if your pool has a sloped bottom? For most purposes, the method described here will work just fine when you need to estimate volume and gallon capacity. If you have a pool with a deep end or a sloped bottom, it is possible to be more precise by sketching out the pool and dividing it into different segments, then calculating the volumes individually and adding them together.

Bryan Trandem

The accompanying diagram shows a pool as if viewed from the side, in cross-section, indicating how you can visualize the pool as two separate areas for the purposes of calculating volume quite precisely.

Another method is simply to measure the pool at the deepest part and at the shallowest part, and take the average of the two measurements as the depth of the pool. This method may be fine if you don't need to be very precise in your calculation.

Round Pool

To calculate the volume of a round pool, again multiply the surface area, as described above, then multiply it times the depth. The 20-foot diameter pool had a surface area of 314 square feet. If this pool is 4 feet deep, the volume would be 1,256 cubic feet.

To convert this measurement to gallons, multiply by 7.48. So, a pool holding 1,256 cubic feet has a gallon capacity of 9,394.88 gallons.

Irregular Curved Pool

With a pool that is kidney shaped or another irregular shape, the method is much the same: Take the estimated surface area and multiply by the depth. Then, take this cubic footage measurement and multiply by 7.48 to arrive at the gallon capacity of your swimming pool.